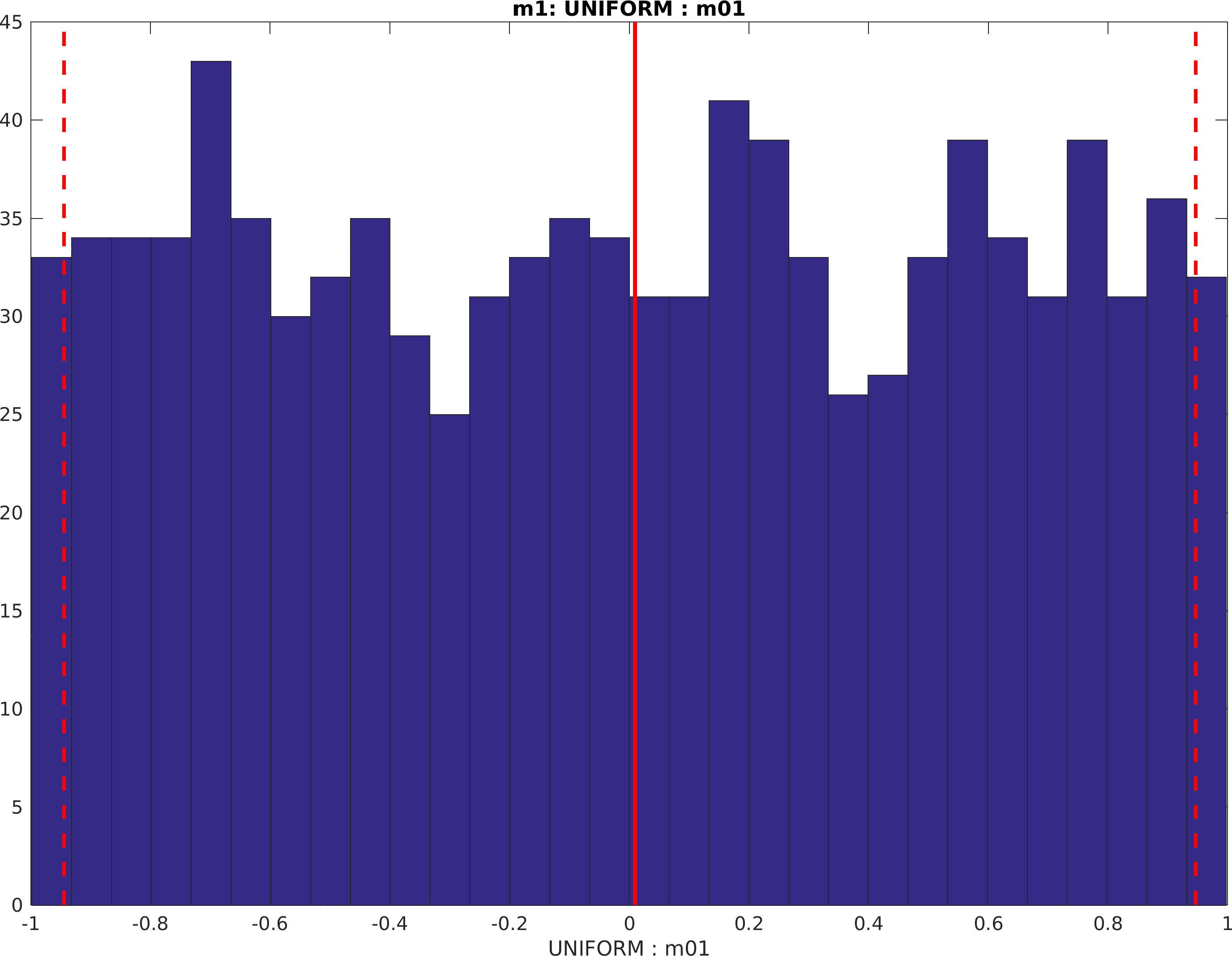
Uniform distribution

A uniform prior model can be specified using the 'uniform' type prior model

prior{1}.type='uniform';

The only parameters needed are the minimum (min) and maximum (max) values. A 1D uniform distribution between -1 and 1 can be specified as

prior{1}.type='uniform';
prior{1}.min=-1;
prior{1}.max=1;

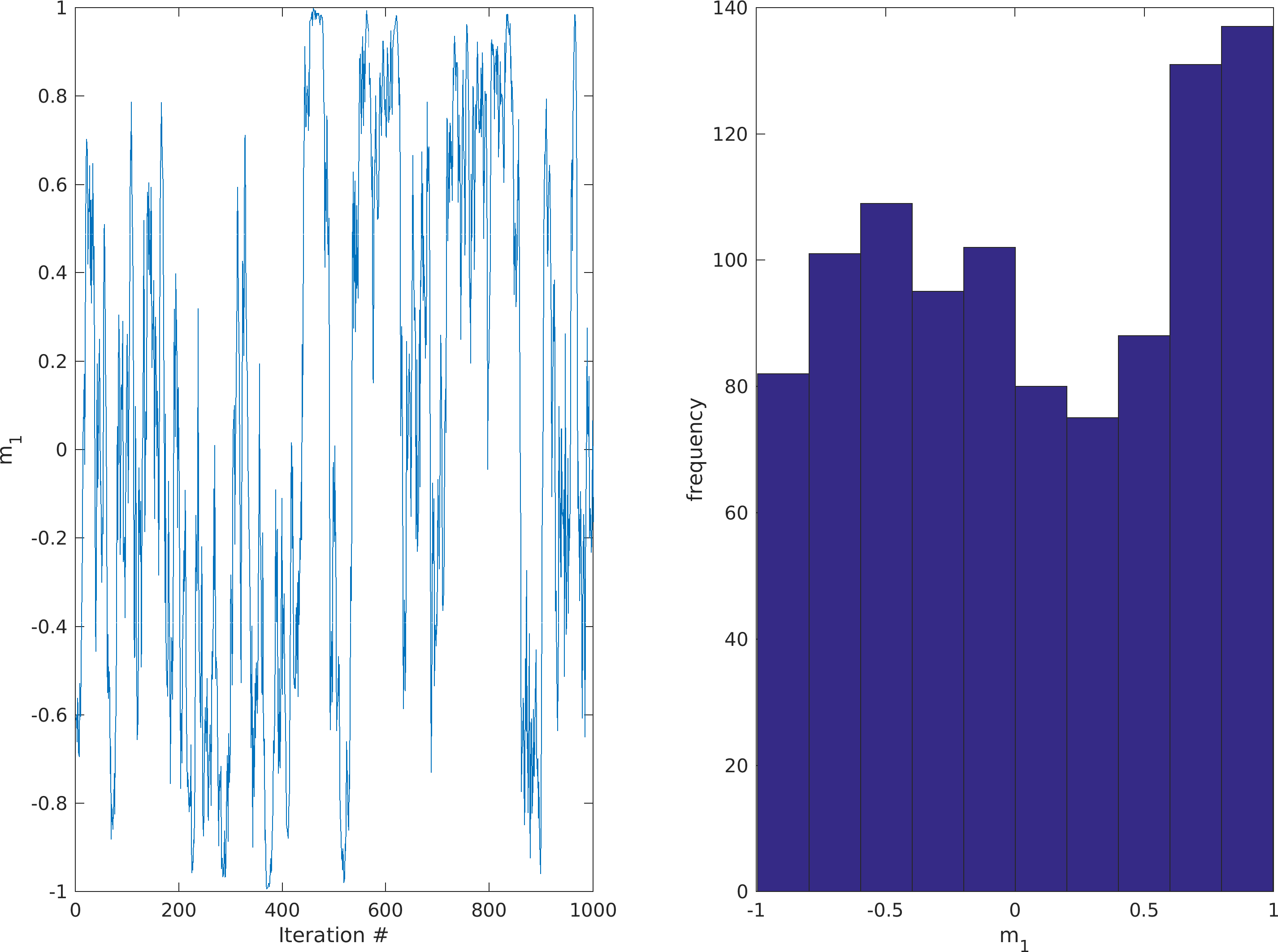
Random walk using sequential Gibbs sampling

A random walk in the uniform prior (as in any supported prior type) can be obtained using sequential Gibbs sampling:

%% seq gibbs
prior{1}.seq_gibbs.step=0.2;
N=1000;
m_all=zeros(1,N);
[m,prior]=sippi_prior(prior);     
for i=1:1000;
     [m,prior]=sippi_prior(prior,m);
     m_all(i)=m{1};
     subplot(1,2,1);plot(1:i,m_all(1:i));
end
xlabel('Iteration #')
ylabel('m_1')

Higher order model

By setting the x, y, and z parameter, a higher order prior (uncorrelated) can be set. For example 3 independent model parameters with a uniform prior distribution between 20 and 50, can be defined as

prior{1}.type='uniform';
prior{1}.x=[1 2 3];
prior{1}.min=20;
prior{1}.max=50;

Note that using the 'uniform' type priori model, is slightly more computational efficient than using a 'gaussian' type prior model with a high norm.